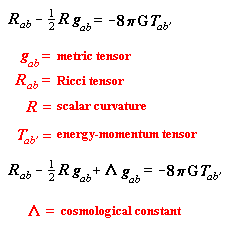Physics Stuff
Odds and Ends for the Classroom and Beyond
Some answers, useful resources and more questions.

Inertial Mass, Mach's principle and Brans-Dicke Theory
By creating a Scalar-tensor theory of gravity in adding a scalar field to the metric of General relativity, mass has not just an effect on geometry but also on Newton's Gravitational constant, G- now not constant but related to Mass and Radius of universe by:
We thus assume the 1/G might be a field, ϕ. The scalar field is related to the universes' mass density according to
Newton's G is now not a constant but a function of age and space of and in the universe. Here is some ideas in it:
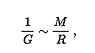

Energy-Momentum as conjugate variables
Conservation of Relativistic mass and thus energy is easily proven by considering an inelastic collision of two bodies while invoking the conservation of momentum. As such the momentum law appears more primitive. Is this somehow an artefact of momentum - space and energy- time as conjugate variables and the implicit necessity to assume causality in constructing such a scenario?

Snell's Law and Einstein's metric of space-time
There is an isomorphism that exists between the refractive index,n (of Snell) and the metric, g (of Einstein): that the isomorphism exists is purely due to the general covariance of Maxwell's equations. A few thoughts in increasing tentativeness:
1. This isomorphism does not require additionally the linearity (superposition of charges) of the electromagnetic waves so would could also infer that we could similarly cloak non-linear gravitational waves by an appropriate mass distribution given the natural covariance of einstein's field equations?
2. We do not need such additional inertial (gravitational) mass cloaking if there were to be some (albeit) contrived ( 3-d annulus or shell that need not itself be electrically charged) mass distribution out in the cosmos to account for some missing (dark) matter.
Brans-Dicke Scalar-Tensor Field Equations of Gravitation:
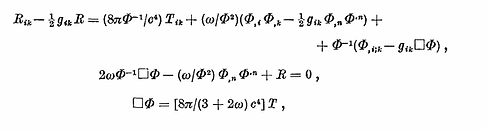
One might think it interesting to consider that Newton's G in Einstein's equations is not a constant but a scalar field; as a variable through space (that is a variable in time). Inertial reference frames in which Newton's mechanics is valid are those from which it is observed that the "fixed stars" to be unaccelerated. Inertial mass is thus according to Mach determined by some coordinate independent (scalar) field would be needed.

Jordan Brans-Dicke Scalar Field Extension of General Relativity
The Weak Equivalence Principle (WEP) merely states that all point particles fall with the same acceleration in a gravitational field.
Sciama, 1953 described a "toy" theory to illustrate a strong version of Mach's Principle drawing from electromagnetism where acceleration of charge induces a force: in pre-relativistic setting the vector potential, A, is induced by current, ρev while the electric force is proportional to the time derivative of A. Sciama's model in which the acceleration of the fixed stars (modeled as a thin, distant, shell) induces a gravitational source for inertial forces. Unlike GR, this vector-based induction of inertial forces cannot be geometrically gauged away.
Consider a Gaussian shell or 3-d annulus mass formation. within that shell no gravitational forces or indeed electromagentic forces act according to Gauss' law.
The inertial mass according to Mach and Brans-Dicke and the likes is determined from such an annulus of all the (receding) stars in the universe. These stars are accelerating away from our test with differentially more rapidly but nevertheless isotropically. Is there any such Machian equivalent principle for magnetic (if not electric) charge where overall neutrality need not be the case in bulk matter distributions? That is can we attribute the magnetic-charged quality attributed to some matter from the bulk magnetic poles that are due to locally anisotropies and inhomogenities in the distribution of matter.