Physics Stuff
Odds and Ends for the Classroom and Beyond
Some answers, useful resources and more questions.

“We know very little, and yet it is astonishing that we know so much, and still more astonishing that so little knowledge can give us so much power.” – Bertrand Russell

The under-handedness of some Invariance Laws
Our universe of Natural Laws, whether unchanging in time or not, obeys a profound set of symmetries. We observe a handedness in Nature that goes deeper than that which differentiates between our opposable thumbs. An object is called "chiral" and possesses a handedness if it cannot be superimposed on its mirror image. Mathematically we say that it cannot be transformed into precisely the same configuration by a parity transformation that inverts the object into its image. Why is this so?
Lucky Linearity of Quantum Mechanics

Algebra of non-commuting matrix multiplication
Classically, the universe behaves in a weakly chaotic manner. All it's clockwork-like cyclicality is mostly illusory. The apparent simple periodicity observed in the universe belies a complex struggle between bifurcations of plausible orbits in the short term against the pull of long-term stability.
That chaos is just a small perturbation away is due to the non-linearity of the (gravitational field) equations describing the systems' trajectories.
The operation of multiplication is said to commute across the integers as the order has no impact on the final result. The order of multiplication of matrices does matter. The set of rotations described by a 3x3 matrix depends on the order in which the transformations are applied.
In the diagram above applying two rotations (multiplying two matrices) in two different orders delivers a different orientation for the book.
Quaternians as Hyper Complex Numbers
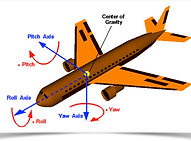
We can view multiplication of one real number by another as merely the expansion (re-scaling) of the 1-dimensional (1-d) Real number line. Multiplication by a complex number then represents rotation in the 2-d Argand plane (right). We then think of quaternians as representing the set of 4 possible manipulations (pitching, rolling and yawing) of an object (as aeroplane below) in 3-d space plus the rescaling of space as for the Reals.
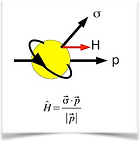
Helicity and Chirality
Mathematically, helicity is the sign of the projection of the spin vector onto the momentum vector: left is negative, right is positive. Helicity is rotationally invariant but for massless particles it also Lorentz invariant so no boosts are possible that will reverse the sign of the 3-momentum of the particle. Helicity is a pseudo scalar changing sign under a Parity transformation. In order to preserve parity in a reaction both potential helictites of the particle need to be present and this is the case for the photon with spin ±1.